Hand-Eye Calibration

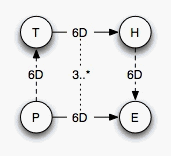
Hand-Eye Calibration is the simulataneous computation of two unknown spatial relationships in a circle of spatial relationships.

The Problem

The hand-eye calibration problem first appeared and got its name from the robotics community, where a camera ("eye") was mounted on the gripper ("hand") of a robot. The cameras was calibrated using a calibration pattern. Then the unknown transformation from the robot coordinate system to the calibration pattern coordinate system as well as the transformation from the camera to the hand coordinate system need to be estimated simultaneously.

Application

Robot-Camera-Calibration (also Tracker-Camera Calibration)

This is the standard "hand-eye calibration" problem: Calculate the camera-sensor transformation X by using several measurements A_i, B_i (that give you A,B).

• Robot Arm with Camera
• Outside-In Tracking System with Inside-Out Tracking System
• Camera with Gyroscope

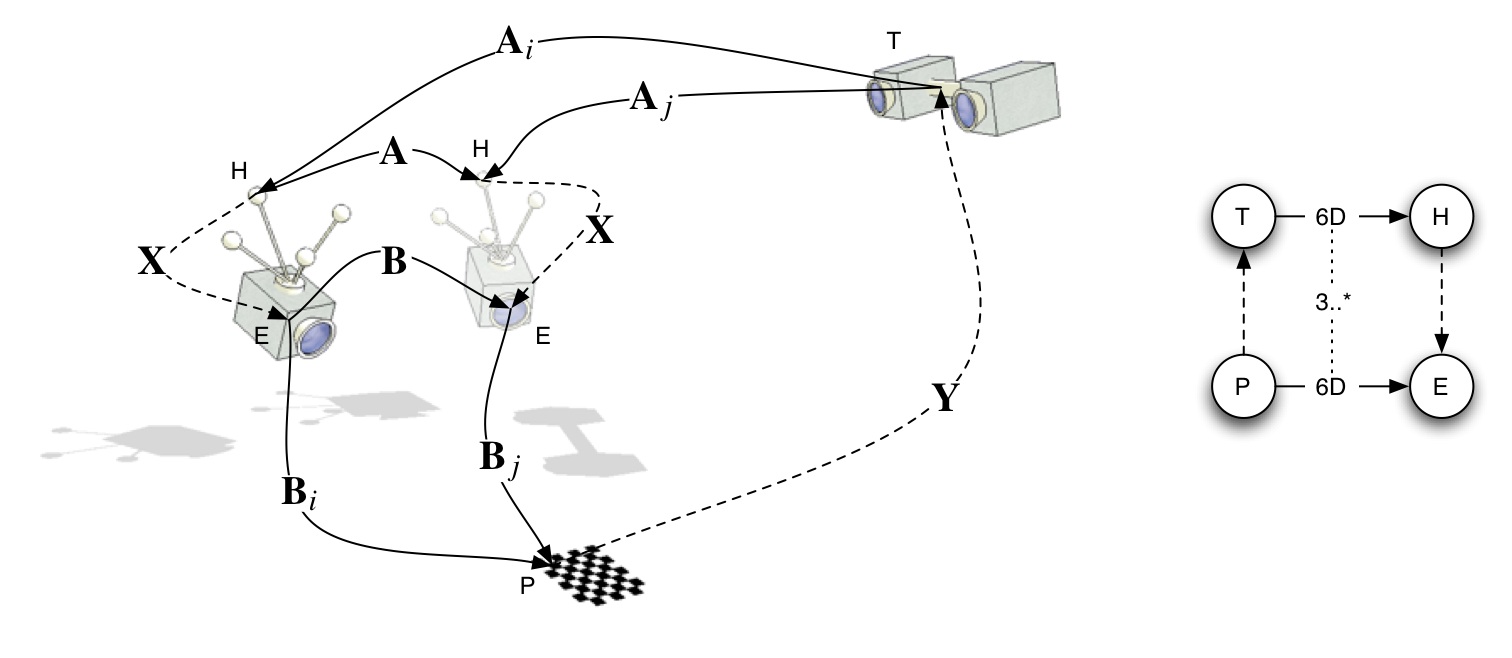
Tracker Alignment

First estimate hand-eye calibration using standard algorithms, then calculate Y from the estimated parameters. Note that the problem is symetric in X and Y.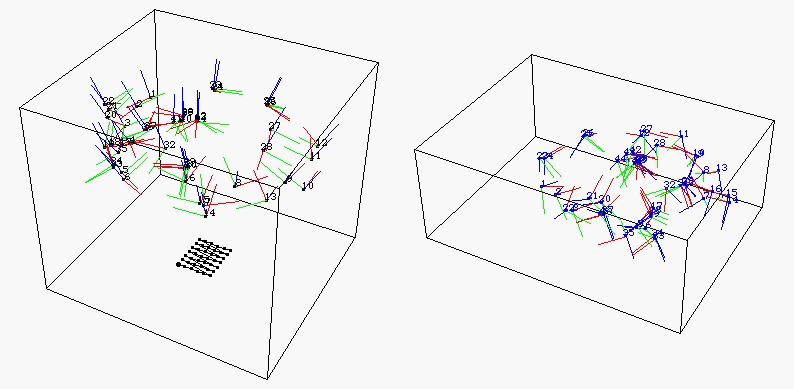

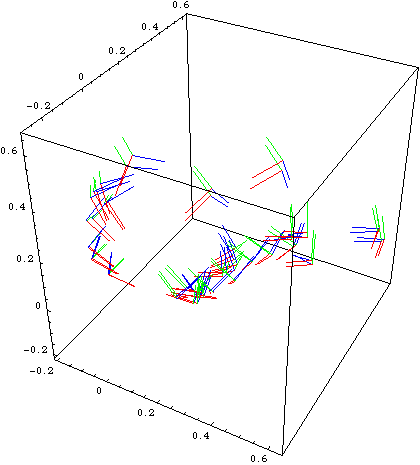We then can either use the Hand-Eye-Calibration methods to estimate X and then Y independently, or use the estimated x to calculate y by closing the loop.

Here we see the collected poses of the eye (left) and the hand (middle) as well as the combined poses after calibration (right)

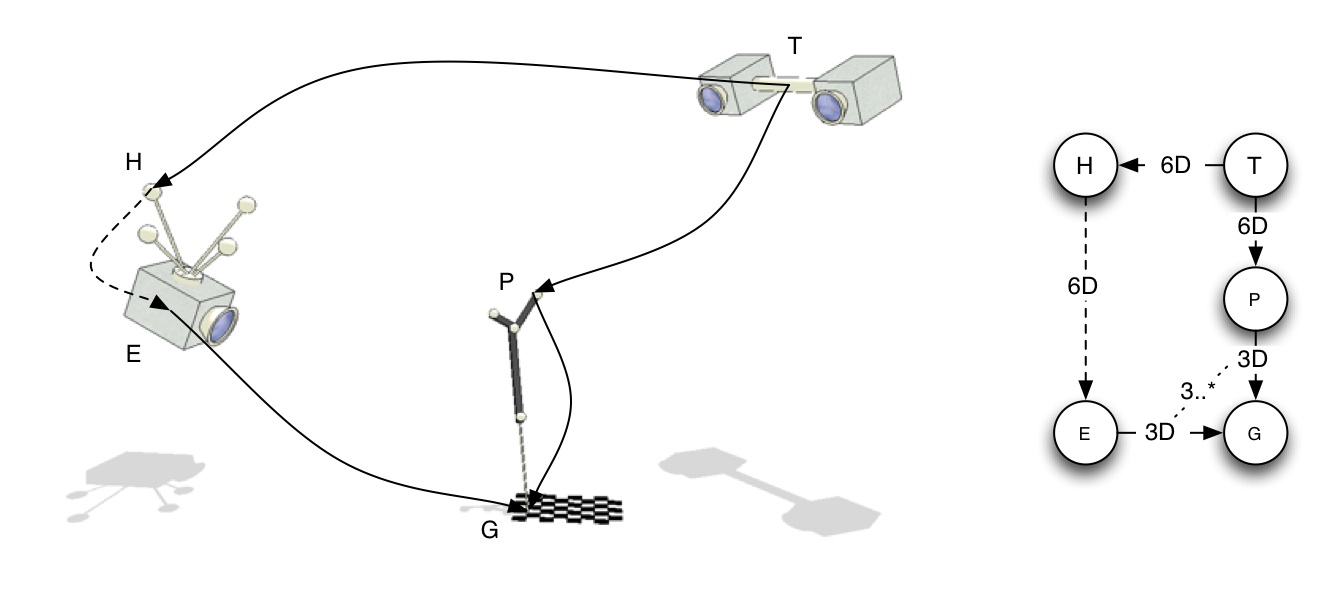
Wrong Uses

Hand-Eye calibration algorithms should not be used when we have a possibility to directly measure one of the two unknown spatial relationships.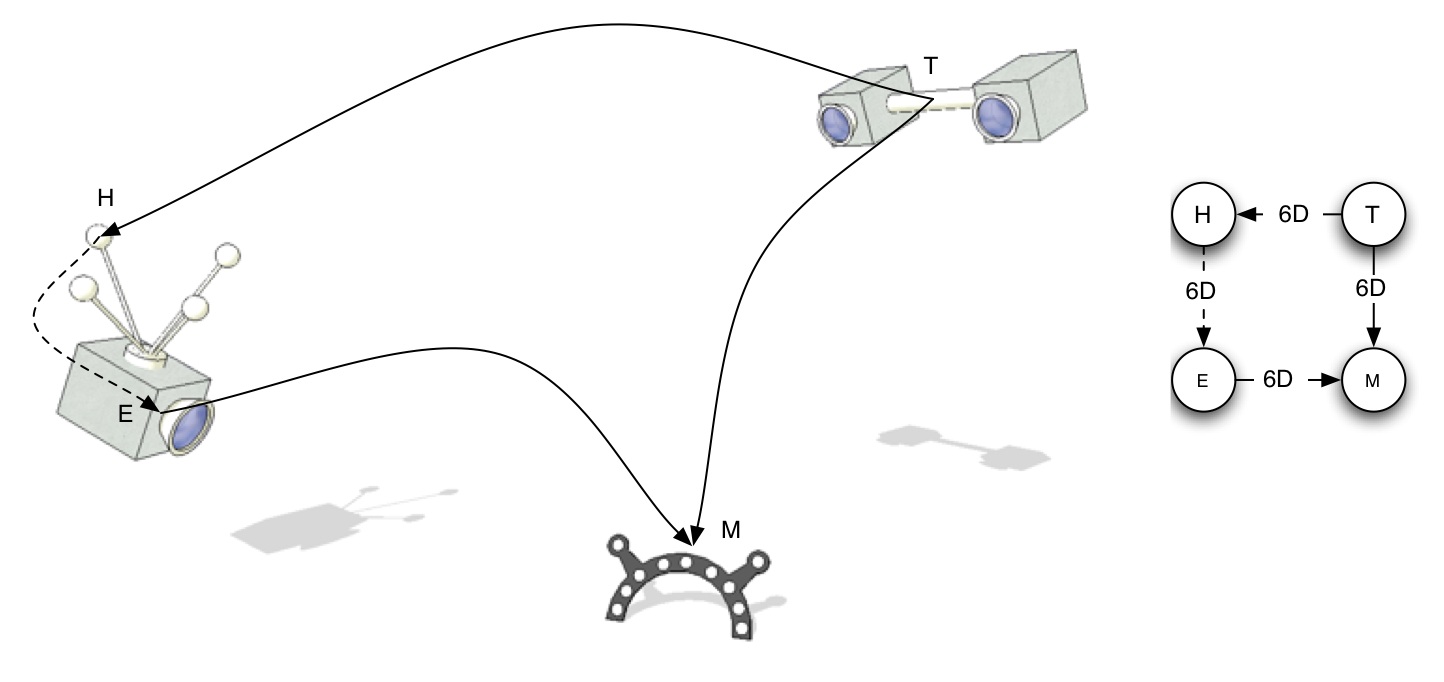

Possible Solutions from the Literature

Roughly, the methods used can be split up into two parts: Most approaches decompose the matrix X into its rotational and translational part and optimize for first the rotation and then the translation. More bibliography can be found at Keith Prices Computer Vision Bibliography.

Determining first the Rotation then the Translation

• The "classic" way, these papers are refered by many later on
  • Tsai, R.Y., Lenz, R.K.
    Real Time Versatile Robotics Hand/Eye Calibration using 3D Machine Vision
    Robotics and Automation, 1988. Proceedings., 1988 IEEE International Conference on
    24-29 April 1988 Page(s):554 - 561 vol.1
    A new technique for fully autonomous and efficient 3D robotics hand/eye calibration
    IEEE Transactions onRobotics and Automation, 5 (3) 1989 p.345-358
  • Shiu, Y.C., Ahmad, S.
    Calibration of wrist-mounted robotic sensors by solving homogeneous transform equations of the form AX=XB
    IEEE Transactions on Robotics and Automation, 5 (1) 1989, p.16-29
• An early comparison of the methods available at that time was given by
  • Wang, C.-C.,
    Extrinsic calibration of a vision sensor mounted on a robot
    IEEE Transactions on Robotics and Automation, 2 (8) 1992, p.161-175

• Another way using quaternionsas rotation representation:
  • Chou, Jack C. K. and Kamel, M.,
    Quaternions Approach to Solve the Kinematic Equation of Rotation of a Sensor-Mounted Robotic Manipulator,
    Proceedings of 1988 IEEE International Conference on Robotics and Automation, Vol. 2, pp. 656-662, 1988
  • Chou, Jack C. K. and Kamel, M.
    Finding the position and orientation of a sensor on a robot manipulator using quaternions.
    International Journal of Robotics Research, 10(3):240-254, June 1991

• Non linear equation system:
  • F. Dornaika and R. Horaud.
    Simultaneous robot-world and hand-eye calibration.
    Robotics and Automation, IEEE Transactions on, 14(4):617–622, 1998.
  • R. Horaud and F. Dornaika.
    Hand-eye calibration.
    International Journal of Robotics Research, 14(3):195–210, 1995.

• Another one using the Euclidean Group
  • F. Park and B. Martin
    Robot Sensor Calibration: Solving AX = XB on the Euclidean Group,
    IEEE Transactions on Robotics and Automation, (10) 1994, p. 717–721

• Y. Baillot, S. Julier, D. Brow, M. Livingston
  A Tracker Alignment Framework for Augmented Reality
  ISMAR 2003, Tokio, Japan
  • claim to provide a "framework" for (a) tracker-to-world registration, (b) tracker-to-tracker registration and (c) locatable-to-display registration. this is not necessarily hand-eye calibration since they focus on Optical-See-Through Displays and therefore probably more related to SPAAM?
  • however, Appendix A shows a solution to the hand-eye calibration problem (which is a sub-problem of theirs).
  • cites hand-eye calibration from: F. Park, B. Martin
    Robot Sensor Calibration: Solving AX=XB on the Euclidian Group.
    IEEE Trans. Rob.Aut. 10(5):717-721, October 1994
  • they seem to use some implicit constraints to calculate the calibration with less than the required two movement pairs.

• Milan Ikits,
  Coregistration of Pose Measurement Devices Using Nonlinear Least Squares Parameter Estimation
  School of Computing Technical Report, UUCS-00-018, University of Utah, December 2000
  • uses standard least-squares solution for first rotation, then translation
  • has a section on computing the a posteriori covariance of the calibration

• Michael Aron, Gilles Simon and Marie-Odile Berger
  Handling uncertain sensor data in vision-based camera tracking
  International Symposium on Mixed and Augmented Reality 2004, Arlington, VA, USA
  • discusses error propagation in hand-eye calibration

• Irene Fassi, Giovanni Legnani,
  Hand to Sensor Calibration: A Geometrical Interpretation of the Matrix Equation AX=XB
  Journal on Robotics Systems 22(9), 497-506 (2005)
  • analyses the euation quite educatively, but then also simply solves first rotation then translation in least squares manner

Determining Rotation and Translation simultaneously

• K. Daniilidis,
  Hand-eye calibration using dual quaternions
  Int. Journ. Robotics Res, 18: 286-298, 1999
  • any rigid transformation can be represented by a rotation φ around some axis and then a translation d along that same axis. This is calles screw.
  • referes to Chassless Theorem
  • uses plücker representation of lines
  • uses dual quaternions to represent the screw
  • a good description of that algorithm can be found in Jochen Schmidt, Florian Vogt, Heinrich Niemann,
    Robust Hand-Eye Calibration of an Endoscopic Surgery Robot Using Dual Quaternions
    Pattern Recognition, 25th DAGM Symposium, LNCS 2781, pages 548-556.
    • also discusses the selection of movement pairs for increased numerical stability and the elimination of outliers
    • Schmidt, Jochen and Vogt, Florian and Niemann, Heinrich
      Vector Quantization Based Data Selection for Hand-Eye Calibration
      In: Girod, B. ; Magnor, M. ; Seidel, H.-P. (Eds.) : Vision, Modeling, and Visualization 2004 (Vision, Modeling, and Visualization 2004 Stanford, USA). Berlin, Amsterdam : Aka / IOS Press, 2004, pp. 21-28.
  • a second paper by the original author:
    Daniilidis, K., Bayro-Corrochano, E.,
    The dual quaternion approach to hand-eye calibration,
    Proceedings of the 13th International Conference on Pattern Recognition, , Vol.1, 25-29 Aug 1996, p.318-322

• N. Andreff, R. Horaud, and B. Espiau
  . On-line hand-eye calibration.
  In Second International Conference on 3-D Digital Imaging and Modeling (3DIM’99), pages 430–436, Ottawa, October 1999.

• H. Zhuang and Y. C. Shiu.
  A noise tolerant algorithm for wrist-mounted robotic sensor calibration with or without sensor orientation measurement
  . In Proceedings of the 1992 lEEE/RSJ International Conference on Intelligent Robots and Systems, volume 2, pages 1095–1100, 1992.
  • _H. Zhuang and Z. Qu_
    A new identification jacobian for robotic hand/eye calibration.
    Systems, Man and Cybernetics, IEEE Transactions on, 24(8):1284–1287, 1994.

• K. H. Strobl and G. Hirzinger.
  Optimal Hand-Eye Calibration
  Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2006), Beijing, China, pp. 4647-4653, October 2006.
  Presents a calibration method for eye-in-hand systems in terms of a parametrization of a stochastic model. A metric on the group of the rigid transformations SE(3) and the corresponding error model are proposed for nonlinear optimization.

Other Works on Hand-Eye Calibration

• Jochen Schmidt, Florian Vogt and Heinrich Niemann
  Calibration–Free Hand–Eye Calibration: A Structure–from–Motion Approach
  Pattern Recognition: 27th DAGM Symposium, Vienna, Austria, August 31 - September 2, 2005, LNCS 3663
  
  • This paper presents an extended hand-eye calibration approach that, in contrast to the standard method, does not require a calibration pattern for determining camera position and orientation. Instead, a structure-from-motion algorithm is applied for obtaining the eye-data that is necessary for computing the unknown hand-eye transformation.
    
• H. Zhuang and A. Melchinger. Calibration of a hand/eye matrix and a connection matrix using relative pose measurements. Proc. of IEEE International Conference on Robotics and Automation, 28(3):369, 1997.

Implementation

If you knw of any other (free) implementation of one of the hand-eye calibration algorithms, feel free to add the link here.

MATLAB

An implementation for MATLAB based on the Camera Calibration Toolbox is available from Christian Wengert, who did his PhD at ETH Zürich.

Another implementation based on the Tsai-Lenz papers you can find on Zoran Lazarevic's homepage.

Mathematica

Assume that the poses of the "hand" and the "eye" are given in the following coordinate system (as seen in the figure above):

• hand poses are given as pose of the hand relative to the tracker coordinate system
• eye poses are given as pose of the calibration pattern relative to the camera coordinate system

First compute the relative motions

   Hc = Flatten[Table[Table[Ait[[j]].Inverse[Ait[[i]]], {j, i+1, Length[Ait]}], {i, Length[Ait]}], 1];
   Hg = Flatten[Table[Table[Inverse[Bit[[j]]].Bit[[i]], {j, i+1, Length[Bit]}], {i, Length[Bit]}], 1];

and from that the matrix X as

   X = HandEyeTsaiLenz[Hg, Hc]

with (Tsai-Lenz 1988)

   Skew[{x_, y_, z_}] := {{0, -z, y}, {z, 0, -x}, {-y, x, 0}}
   HandEyeTsaiLenz[Hg_, Hc_] := Module[{Pg, Pc, lefthand, righthand},
      Pg = Drop[MatrixToQuaternion[#1], 1] & /@ Hg; 
      Pc = Drop[MatrixToQuaternion[#1], 1] & /@ Hc;
    
      (* Solve for the rotational part *)
      lefthand = Flatten[Skew /@ (Pc + Pg), 1];
      righthand =  Flatten[Pc - Pg, 1];
      Pcg = PseudoInverse[lefthand].righthand;
      Pcg = 2/Sqrt[1 + Pcg.Pcg] Pcg;
      Rcg = (1 - 0.5 (Pcg.Pcg))IdentityMatrix[3] + 0.5 *( (Transpose[{Pcg}].{Pcg}) + Sqrt[4 - Pcg.Pcg] Skew[Pcg]);
    
      (* Solve for the translational part *)
      lefthand = Flatten[ (#[[Range[3], Range[3]]] - 
      IdentityMatrix[3]) & /@ Hg, 1];
      righthand = Flatten[(Rcg.(#[[Range[3], 4]]) & /@ Hc), 1] - Flatten[(#[[Range[3], 4]]) & /@ Hg, 1];
      (* Print[lefthand, ". x =", Transpose[{righthand}]]; *)
      Tcg = PseudoInverse[lefthand].righthand;
      Append[Transpose[Append[Transpose[Rcg], Tcg]], {0, 0, 0, 1}]
    ]

Tips & Tricks

• Coordinate Systems: Make sure that all your coordinate systems you are using are right-handed (or left-handed, but never mixed). Also have a close look at the direction of the transformation the tracking systems are providing; you might need to invert one of the motions before applying the calibration.