Diplomarbeit: Level Sets for Symbolic Reconstruction
Student: Jakob VogelAdvisor: Prof. Dr. Nassir Navab
Supervision by: Andreas Keil
Abstract
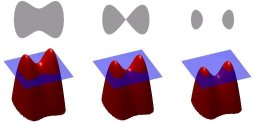
The task of segmenting medical image data often can be carried out by using basic algorithms like region growing, e.g. There are, however, clinical questions which give rise to advanced segmentation problems. In order to solve those problems, more sophisticated algorithmic approaches have to be applied. One of them is called "Level Sets" and provides the programmer with a lot of options to define his segmentation goals. The segmentation is achieved by adjusting region boundaries. These adjustments are driven by user-defined energies and forces. Minimizing those energies leads to partial differential equations which – in the end – have to be solved using finite differences. The boundaries are represented implicitely, defining them as the zero level set (hence the name) of some function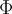 :
:
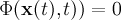
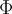 :
:
Resources and Literature
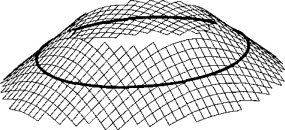
Figure 2: Narrow band around some boundary, Source: [3]
- [1] J.A. Sethian. Level Set Methods and Fast Marching Methods. Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science. Cambridge University Press, 2nd edition, 1999; download of introduction, chapter 1, and bibliography
- [2] J.A. Sethian's excellent web resource
- [3] D. Adalsteinsson and J.A. Sethian. A fast level set method for propagating interfaces. J. Computational Physics, 118(2):269-277, 1995. doi:10.1006/jcph.1995.1098
- [4] R. Malladi, J.A. Sethian, and B.C. Vemuri. Shape modeling with front propagation: A level set approach. IEEE Trans. Pattern Anal. Machine Intell., 17(2):158-175, 1995. doi:10.1109/34.368173
Documents
| Students.ProjectForm | |
|---|---|
| Title: | Level Sets for Symbolic Reconstruction |
| Abstract: | One of the more sophisticated segmentation methods is called "Level Set Method". It provides the programmer with a lot of options to define his segmentation goals. The segmentation is achieved by adjusting region boundaries. These adjustments are driven by user-defined forces. All this leads to partial differential equations which, in the end, have to be solved using finite differences. The IDP consists of implementing numerical solvers for PDEs arising from Level Set Methods. The PDEs are discretized using finite differences and solved with usual schemes thereafter. The only difference to usual solvers is that so-called "Narrow Band Methods" can be applied which operate on a local band around border pixels only, thereby reducing the workload dramatically. The IDP starts with an evaluation of existing narrow band implementations. Some selected methods will then be implemented by programming a new solver. Finally, the implementation has to be evaluated and tested extensively. The student should seek an IDP in mathematics and have some knowledge about the numerical solution of PDEs. This knowledge can be gained by attending the math lectures on Numerical Mathematics of PDEs (usually called "Numerik 4" at TUM) or sth. comparable. Knowledge about the theory of PDEs is not required. |
| Student: | Jakob Vogel |
| Director: | Nassir Navab |
| Supervisor: | Andreas Keil |
| Type: | Diploma Thesis |
| Area: | Segmentation, Medical Imaging, Computer Vision |
| Status: | finished |
| Start: | 2009/01/15 |
| Finish: | 2009/09/30 |
| Thesis (optional): | |
| Picture: | |
| I | Attachment  | Action  | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|
| | jakob-final-presentation.pdf | manage | 5970.3 K | 02 Oct 2009 - 17:24 | AndreasKeil |