Tumor Induced Brain Deformaitons
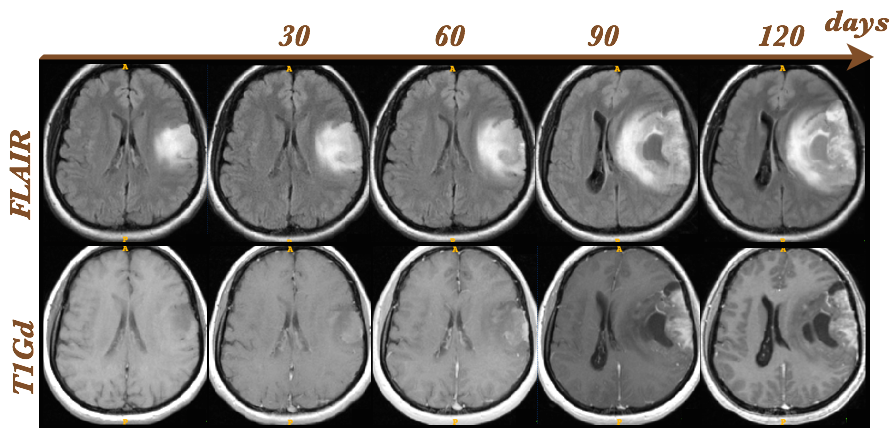 Figure 1: Evolution of the tumour and corresponding tissue displacement and compression over time, shown on two different image modalities. T1Gd MRI scan show the vascularised part of the tumour and necrotic core. FLAIR MRI scan enhance lesions’ oedema.
Figure 1: Evolution of the tumour and corresponding tissue displacement and compression over time, shown on two different image modalities. T1Gd MRI scan show the vascularised part of the tumour and necrotic core. FLAIR MRI scan enhance lesions’ oedema.
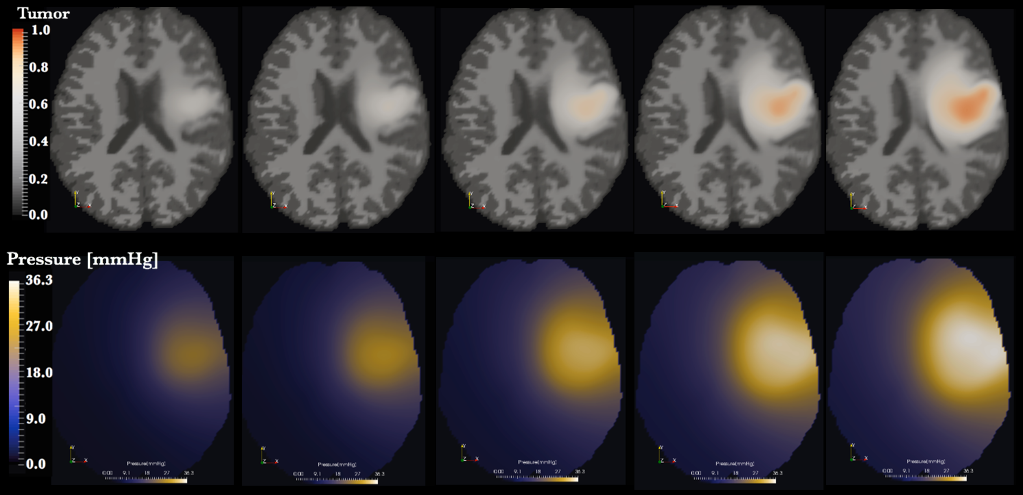 Figure 2: Simulation of the tumour growth and mechanical interaction with the surrounding anatomy (first row). Increase of the intracranial pressure caused by the growing tumour (second row).
Figure 2: Simulation of the tumour growth and mechanical interaction with the surrounding anatomy (first row). Increase of the intracranial pressure caused by the growing tumour (second row).
|
Project Description
Glioma is the most common type of primary brain tumours. It is characterised by aggressive growth and poor prognosis. An increased intracranial pressure is the most critical symptom, leading to tissue and nerve compression, and often is the main cause of death. Clinical interventions would benefit from computational predictions of the tumour growth and corresponding mass effect. However, conventional mechanistic models can not provide personalised prognosis, since they are based on model parameters, which patient and disease specific values can not be inferred in a non invasive way. We present a novel approach for modelling tumour induced brain deformations and corresponding increase of the intracranial pressure in the patient individual anatomy reconstructed from the medical scans. The presented mechanistic model is based on tissue displacement detectable from medical images (see Figure 1), allowing for an easy model personalisation. Calibrated model can be used to predict onset of critical conditions and thus assist clinical interventions (see Figure 2). Furthermore, the model can be easily extended to account for post surgery brain mechanics (i.e. relaxation of the compressed tissue after tumour resection).
Tasks
- Application of the existing model to patient’s brain anatomy
- Model calibration with respect to patient specific conditions
- Extension of the existing model to account for post-surgical brain dynamics (i.e. relaxation of the compressed tissue)
Requirements
- Good Programming Skills (C++)
- Basics of Numerical Analysis (Finite differences, integration schemes)
- Basics of Continuum Mechanics
- Basics of parallel programming (not necessary but is an advantage)
- Desire to Learn and Improvise
- Independent worker
|
|
Contact
If you are interested in the project or if you have any questions please contact
 Figure 1: Evolution of the tumour and corresponding tissue displacement and compression over time, shown on two different image modalities. T1Gd MRI scan show the vascularised part of the tumour and necrotic core. FLAIR MRI scan enhance lesions’ oedema.
Figure 1: Evolution of the tumour and corresponding tissue displacement and compression over time, shown on two different image modalities. T1Gd MRI scan show the vascularised part of the tumour and necrotic core. FLAIR MRI scan enhance lesions’ oedema.
 Figure 2: Simulation of the tumour growth and mechanical interaction with the surrounding anatomy (first row). Increase of the intracranial pressure caused by the growing tumour (second row).
Figure 2: Simulation of the tumour growth and mechanical interaction with the surrounding anatomy (first row). Increase of the intracranial pressure caused by the growing tumour (second row).